Introduction to differentiable manifolds in SageMath

by Andrzej Chrzeszczyk

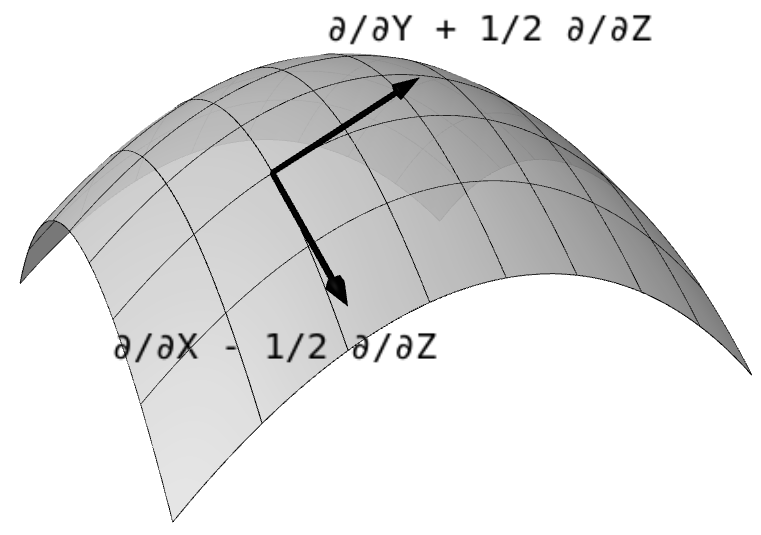
tangent_vectors figure generated by notebook 8

  1. Basic notions of topology
  2. Examples of charts. Cartesian and spherical coordinates
  3. Function graph as a manifold
  4. Spheres as manifolds
  5. Spheres and spherical coordinates in higher dimensions
  6. The notion of module
  7. Smooth functions and pullbacks
  8. Tangent spaces
  9. a. Tensors on modules
  1. Tensors on TpM
  2. Alternating forms on modules
  3. Vector fields
  4. Vector fields - continuation
  5. Tensor fields
  6. Differential k-forms
  7. Pulback of tensor fields
  8. Exterior derivative
  9. One-parameter groups of transformations
  10. Integral curves
  11. Lie derivative
  12. Integration of differential forms on singular k-cubes
  13. Connection
  14. Riemannian and pseudo-Riemannian manifolds
  15. Curvature
  16. Riemannian curvature tensor of type (0,4)
  17. Torsion and curvature forms