Gravitational radiation by a blob of matter¶
Gravitational radiation by a blob of matter on a circular orbit around a Kerr black hole
This module implements the following functions:
h_blob(): evaluates \(r h_+\) or \(r h_\times\)h_blob_signal(): time sequence of \(r h_+/\mu\) or \(r h_\times/\mu\)h_toy_model_semi_analytic(): \(r h_+/\mu\) and \(r h_\times/\mu\) from a semi-analytic approximation based on a constant density blobsurface_density_toy_model(): \(\Sigma(\bar{r},\bar{\phi})\) as an indicator functionsurface_density_gaussian(): \(\Sigma(\bar{r},\bar{\phi})\) as a Gaussian profileblob_mass(): mass of the blob of matter, by integration of \(\Sigma(\bar{r},\bar{\phi})\)
- kerrgeodesic_gw.gw_blob.blob_mass(a, surf_dens, param_surf_dens, integ_range, epsabs=1e-08, epsrel=1e-08)¶
Compute the mass of a blob of matter by integrating its surface density.
INPUT:
a– BH angular momentum parameter (in units of \(M\))surf_dens– surface density function \(\Sigma\); must take three arguments:(r_bar, phi_bar, param_surf_dens), wherer_baris the Boyer-Lindquist radial coordinate \(\bar{r}\) in the matter blobphi_baris the Boyer-Lindquist azimuthal coordinate \(\bar{\phi}\) in the matter blobparam_surf_densare parameters defining the function \(\Sigma(\bar{r},\bar{\phi})\)
param_surf_dens– parameters to be passed as the third argument to the functionsurf_dens(see above)integ_range– tuple \((\bar{r}_1, \bar{r}_2, \bar{\phi}_1, \bar{\phi}_2)\) defining the integration rangeepsabs– (default: 1e-8) absolute tolerance of the inner 1-D quadrature integrationepsrel– (default: 1e-8) relative tolerance of the inner 1-D integrals
OUTPUT:
a pair
(mu, err), wheremuis the mass of the matter blob anderris an estimate of the absolute error in the computation of the integral
EXAMPLES:
sage: from kerrgeodesic_gw import blob_mass, surface_density_gaussian sage: param = [6.5, 0., 0.3] sage: integ_range = [6, 7, -0.1, 0.1] sage: blob_mass(0., surface_density_gaussian, param, integ_range) # tol 1.0e-13 (0.3328779622200767, 5.671806593829388e-10) sage: blob_mass(0., surface_density_gaussian, param, integ_range, # tol 1.0e-13 ....: epsabs=1.e-3) (0.33287796222007715, 1.109366597806814e-06)
- kerrgeodesic_gw.gw_blob.h_blob(u, theta, phi, a, surf_dens, param_surf_dens, integ_range, mode='+', l_max=10, m_min=1, epsabs=1e-06, epsrel=1e-06)¶
Return the rescaled value of \(h_+\) or \(h_\times\) (depending on the parameter
mode) for the gravitational radiation emitted by a matter blob in circular orbit around a Kerr black hole.INPUT:
u– retarded time coordinate of the observer (in units of \(M\), the BH mass): \(u = t - r_*\), where \(t\) is the Boyer-Lindquist time coordinate and \(r_*\) is the tortoise coordinatetheta– Boyer-Lindquist colatitute \(\theta\) of the observerphi– Boyer-Lindquist azimuthal coordinate \(\phi\) of the observera– BH angular momentum parameter (in units of \(M\))surf_dens– surface density function \(\Sigma\); must take three arguments:(r_bar, phi_bar, param_surf_dens), wherer_baris the Boyer-Lindquist radial coordinate \(\bar{r}\) in the matter blobphi_baris the Boyer-Lindquist azimuthal coordinate \(\bar{\phi}\) in the matter blobparam_surf_densare parameters defining the function \(\Sigma(\bar{r},\bar{\phi})\)
param_surf_dens– parameters to be passed as the third argument to the functionsurf_dens(see above)integ_range– tuple \((\bar{r}_1, \bar{r}_2, \bar{\phi}_1, \bar{\phi}_2)\) defining the integration rangemode– (default:'+') string determining which GW polarization mode is considered; allowed values are'+'and'x', for respectively \(h_+\) and \(h_\times\)l_max– (default: 10) upper bound in the summation over the harmonic degree \(\ell\)m_min– (default: 1) lower bound in the summation over the Fourier mode \(m\)epsabs– (default: 1e-6) absolute tolerance passed directly to the inner 1-D quadrature integrationepsrel– (default: 1e-6) relative tolerance of the inner 1-D integrals
OUTPUT:
a pair
(rh, err), whererhis the rescaled waveform \(r h_+\) (resp. \(r h_\times\)) ifmode='+'(resp.'x') , \(r\) being the Boyer-Lindquist radial coordinate of the observer, anderris an estimate of the absolute error in the computation of the integral
EXAMPLES:
Gravitational emission \(h_+\) from a constant density blob close to the ISCO of a Schwarzschild black hole:
sage: from kerrgeodesic_gw import h_blob, surface_density_toy_model sage: a = 0 sage: param_surf_dens = [6.5, 0, 0.6, 0.1] sage: integ_range = [6.3, 6.7, -0.04, 0.04] sage: h_blob(0., pi/2, 0., a, surface_density_toy_model, # tol 1.0e-13 ....: param_surf_dens, integ_range) (0.03688373245628765, 9.872900827148663e-10) sage: h_blob(0., pi/2, 0., a, surface_density_toy_model, # tol 1.0e-13 ....: param_surf_dens, integ_range, l_max=5) (0.037532424224875585, 1.3788099591183387e-09)
The \(h_\times\) part at \(\theta=\pi/4\):
sage: h_blob(0., pi/4, 0., a, surface_density_toy_model, # tol 1.0e-13 ....: param_surf_dens, integ_range, mode='x') (0.06203815455135455, 1.972915290337975e-09) sage: h_blob(0., pi/4, 0., a, surface_density_toy_model, # tol 1.0e-13 ....: param_surf_dens, integ_range, mode='x', l_max=5) (0.06121422594295032, 1.924590678064715e-09)
- kerrgeodesic_gw.gw_blob.h_blob_signal(u_min, u_max, theta, phi, a, surf_dens, param_surf_dens, integ_range, mode='+', nb_points=100, l_max=10, m_min=1, epsabs=1e-06, epsrel=1e-06, store=None, verbose=True)¶
Return a time sequence of \(h_+\) or \(h_\times\) (depending on the parameter
mode) describing the gravitational radiation from a matter blob orbiting a Kerr black hole.INPUT:
u_min– lower bound of the retarded time coordinate of the observer (in units of \(M\), the BH mass): \(u = t - r_*\), where \(t\) is the Boyer-Lindquist time coordinate and \(r_*\) is the tortoise coordinateu_max– upper bound of the retarded time coordinate of the observer (in units of \(M\))theta– Boyer-Lindquist colatitute \(\theta\) of the observerphi– Boyer-Lindquist azimuthal coordinate \(\phi\) of the observera– BH angular momentum parameter (in units of \(M\))surf_dens– surface density function \(\Sigma\); must take three arguments:(r_bar, phi_bar, param_surf_dens), wherer_baris the Boyer-Lindquist radial coordinate \(\bar{r}\) in the matter blobphi_baris the Boyer-Lindquist azimuthal coordinate \(\bar{\phi}\) in the matter blobparam_surf_densare parameters defining the function \(\Sigma(\bar{r},\bar{\phi})\)
param_surf_dens– parameters to be passed as the third argument to the functionsurf_dens(see above)integ_range– tuple \((\bar{r}_1, \bar{r}_2, \bar{\phi}_1, \bar{\phi}_2)\) defining the integration rangemode– (default:'+') string determining which GW polarization mode is considered; allowed values are'+'and'x', for respectively \(h_+\) and \(h_\times\)nb_points– (default: 100) number of points in the interval(u_min, u_max)l_max– (default: 10) upper bound in the summation over the harmonic degree \(\ell\)m_min– (default: 1) lower bound in the summation over the Fourier mode \(m\)epsabs– (default: 1e-6) absolute tolerance passed directly to the inner 1-D quadrature integrationepsrel– (default: 1e-6) relative tolerance of the inner 1-D integralsstore– (default:None) string containing a file name for storing the time sequence; ifNone, no storage is attemptedverbose– (default:True) boolean determining whether to monitor the progress of the sequence computation
OUTPUT:
a list of
nb_pointspairs \((u, r h_+/\mu)\) or \((u, r h_\times/\mu)\) (depending onmode), where \(\mu\) is the blob’s mass and \(r\) is the Boyer-Lindquist radial coordinate of the observer
EXAMPLES:
\(h_+\) sequence for a Gaussian-density matter blob around a Schwarzschild black hole:
sage: from kerrgeodesic_gw import h_blob_signal, surface_density_gaussian sage: param_surf_dens = [6.5, 0., 0.3] sage: integ_range = [6, 7, -0.1, 0.1] sage: a = 0 sage: h_blob_signal(0., 100., pi/4, 0., a, surface_density_gaussian, # tol 1.0e-13 ....: param_surf_dens, integ_range, nb_points=5, ....: epsrel=1e-4, verbose=False) [(0.000000000000000, 0.2988585811681569), (25.0000000000000, -0.3902717353505495), (50.0000000000000, 0.4196374371978159), (75.0000000000000, -0.4729306367862637), (100.000000000000, 0.3464193312741741)]
The corresponding \(h_\times\) sequence:
sage: h_blob_signal(0., 100., pi/4, 0., a, surface_density_gaussian, # tol 1.0e-13 ....: param_surf_dens, integ_range, mode='x', ....: nb_points=5, epsrel=1e-4, verbose=False) [(0.000000000000000, 0.24810446643240472), (25.0000000000000, -0.060862007486422516), (50.0000000000000, -0.12309577666126706), (75.0000000000000, -0.0017707729883368948), (100.000000000000, 0.08100026787377135)]
- kerrgeodesic_gw.gw_blob.h_toy_model_semi_analytic(u, theta, phi, a, r0, phi0, lam, Dphi, l_max=10)¶
Return the gravitational wave emitted by a matter blob orbiting a Kerr black hole (semi-analytic computation based on a toy model surface density).
The surface density of the matter blob is that given by
surface_density_toy_model().The gravitational wave is computed according to the formula
\[h = \frac{2\mu}{r} \, \sum_{\ell=2}^{\infty} \sum_{m=-\ell}^\ell \frac{Z^\infty_{\ell m}(r_0)}{(m\omega_0)^2} \; \text{sinc}\left( \frac{m}{2} \Delta\varphi \right) \, \text{sinc}\left( \frac{3}{4} \varepsilon \, m \omega_0 (1-a\omega_0)u \right) e^{- i m (\omega_0 u + \phi_0)} \, _{-2}S_{\ell m}^{a m \omega_0}(\theta,\varphi)\]INPUT:
u– retarded time coordinate of the observer (in units of \(M\), the BH mass): \(u = t - r_*\), where \(t\) is the Boyer-Lindquist time coordinate and \(r_*\) is the tortoise coordinatetheta– Boyer-Lindquist colatitute \(\theta\) of the observerphi– Boyer-Lindquist azimuthal coordinate \(\phi\) of the observera– BH angular momentum parameter (in units of \(M\))r0– mean radius \(r_0\) of the matter blob (Boyer-Lindquist coordinate)phi0– mean azimuthal angle \(\phi_0\) of the matter blob (Boyer-Lindquist coordinate)lam– radial extent \(\lambda\) of the matter blobDphi– opening angle \(\Delta\phi\) of the matter blobl_max– (default: 10) upper bound in the summation over the harmonic degree \(\ell\)
OUTPUT:
a pair
(hp, hc), wherehp(resp.hc) is \((r / \mu) h_+\) (resp. \((r / \mu) h_\times\)), \(\mu\) being the blob’s mass and \(r\) is the Boyer-Lindquist radial coordinate of the observer
EXAMPLES:
Schwarzschild black hole:
sage: from kerrgeodesic_gw import h_toy_model_semi_analytic sage: a = 0 sage: r0, phi0, lam, Dphi = 6.5, 0, 0.6, 0.1 sage: u = 60. sage: h_toy_model_semi_analytic(u, pi/4, 0., a, r0, phi0, lam, Dphi) # tol 1.0e-13 (0.2999183296797872, 0.36916647790743246) sage: hp, hc = _
Comparison with the exact value:
sage: from kerrgeodesic_gw import (h_blob, blob_mass, ....: surface_density_toy_model) sage: param_surf_dens = [r0, phi0, lam, Dphi] sage: integ_range = [6.2, 6.8, -0.05, 0.05] sage: mu = blob_mass(a, surface_density_toy_model, param_surf_dens, ....: integ_range)[0] sage: hp0 = h_blob(u, pi/4, 0., a, surface_density_toy_model, ....: param_surf_dens, integ_range)[0] / mu sage: hc0 = h_blob(u, pi/4, 0., a, surface_density_toy_model, ....: param_surf_dens, integ_range, mode='x')[0] / mu sage: hp0, hc0 # tol 1.0e-13 (0.2951163078053617, 0.3743683023327848) sage: (hp - hp0) / hp0 # tol 1.0e-13 0.01627162494047128 sage: (hc - hc0) / hc0 # tol 1.0e-13 -0.013894938201066784
- kerrgeodesic_gw.gw_blob.surface_density_gaussian(r, phi, param)¶
Surface density of a matter blob with a Gaussian profile
INPUT:
r– Boyer-Lindquist radial coordinate \(\bar{r}\) in the matter blobphi– Boyer-Lindquist azimuthal coordinate \(\bar{\phi}\) in the matter blobparam– list of parameters defining the position and width of matter blob:param[0]: mean radius \(r_0\) (Boyer-Lindquist coordinate)param[1]: mean azimuthal angle \(\phi_0\) (Boyer-Lindquist coordinate)param[2]: width \(\lambda\) of the Gaussian profileparam[3](optional): amplitude \(\Sigma_0\); if not provided, then \(\Sigma_0=1\) is used
OUTPUT:
surface density \(\Sigma(\bar{r}, \bar{\phi})\)
EXAMPLES:
sage: from kerrgeodesic_gw import surface_density_gaussian sage: param = [6.5, 0., 0.3] sage: surface_density_gaussian(6.5, 0, param) 1.0 sage: surface_density_gaussian(8., 0, param) # tol 1.0e-13 1.3887943864964021e-11 sage: surface_density_gaussian(6.5, pi/16, param) # tol 1.0e-13 1.4901161193847656e-08
3D representation: \(z=\Sigma(\bar{r}, \bar{\phi})\) in terms of \(x:=\bar{r}\cos\bar\phi\) and \(y:=\bar{r}\sin\bar\phi\):
sage: s_plot = lambda r, phi: surface_density_gaussian(r, phi, param) sage: r, phi, z = var('r phi z') sage: plot3d(s_plot, (r, 6, 8), (phi, -0.4, 0.4), ....: transformation=(r*cos(phi), r*sin(phi), z)) Graphics3d Object
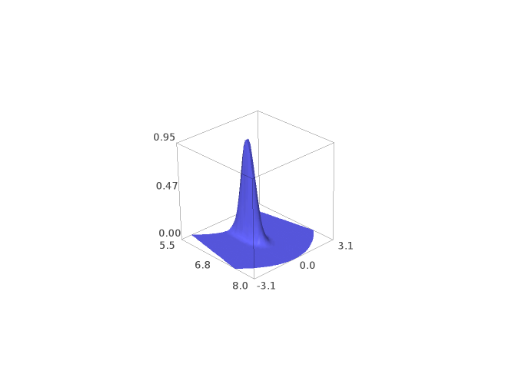
Use with a non-default amplitude (\(\Sigma_0=10^{-5}\)):
sage: sigma0 = 1.e-5 sage: param = [6.5, 0., 0.3, sigma0] sage: surface_density_gaussian(6.5, 0, param) 1e-05
- kerrgeodesic_gw.gw_blob.surface_density_toy_model(r, phi, param)¶
Surface density of the toy model matter blob.
INPUT:
r– Boyer-Lindquist radial coordinate \(\bar{r}\) in the matter blobphi– Boyer-Lindquist azimuthal coordinate \(\bar{\phi}\) in the matter blobparam– list of parameters defining the position and extent of the matter blob:param[0]: mean radius \(r_0\) (Boyer-Lindquist coordinate)param[1]: mean azimuthal angle \(\phi_0\) (Boyer-Lindquist coordinate)param[2]: radial extent \(\lambda\)param[3]: opening angle \(\Delta\phi\)param[4](optional): amplitude \(\Sigma_0\); if not provided, then \(\Sigma_0=1\) is used
OUTPUT:
surface density \(\Sigma(\bar{r}, \bar{\phi})\)
EXAMPLES:
Use with the default amplitude (\(\Sigma_0=1\)):
sage: from kerrgeodesic_gw import surface_density_toy_model sage: param = [6.5, 0, 0.6, 0.1] sage: surface_density_toy_model(6.5, 0, param) 1.0 sage: surface_density_toy_model(6.7, -0.04, param) 1.0 sage: surface_density_toy_model(6.3, 0.04, param) 1.0 sage: surface_density_toy_model(7, -0.06, param) 0.0 sage: surface_density_toy_model(5., 0.06, param) 0.0
3D representation: \(z=\Sigma(\bar{r}, \bar{\phi})\) in terms of \(x:=\bar{r}\cos\bar\phi\) and \(y:=\bar{r}\sin\bar\phi\):
sage: s_plot = lambda r, phi: surface_density_toy_model(r, phi, param) sage: r, phi, z = var('r phi z') sage: plot3d(s_plot, (r, 6, 8), (phi, -0.4, 0.4), ....: transformation=(r*cos(phi), r*sin(phi), z)) Graphics3d Object
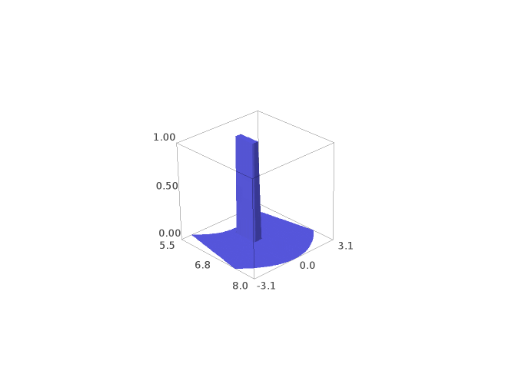
Use with a non-default amplitude (\(\Sigma_0=2\)):
sage: sigma0 = 2. sage: param = [6.5, 0, 0.6, 0.1, sigma0] sage: surface_density_toy_model(6.5, 0, param) 2.0