LISA Detector¶
Functions relative to the LISA detector.
- kerrgeodesic_gw.lisa_detector.power_spectral_density(freq)¶
Return the effective power spectral density (PSD) of the detector noise at a given frequency.
INPUT:
freq– frequency \(f\) (in \(\mathrm{Hz}\))
OUTPUT:
effective power spectral density \(S(f)\) (in \(\mathrm{Hz}^{-1}\))
EXAMPLES:
sage: from kerrgeodesic_gw import lisa_detector sage: Sn = lisa_detector.power_spectral_density sage: Sn(1.e-1) # tol 1.0e-13 3.3944027493062926e-39 sage: Sn(1.e-2) # tol 1.0e-13 2.738383947022306e-40 sage: Sn(1.e-3) # tol 1.0e-13 3.269807574220045e-38
- kerrgeodesic_gw.lisa_detector.power_spectral_density_RCLfit(freq)¶
Return the effective power spectral density (PSD) of the detector noise at a given frequency, according to the analytical fit by Robson, Cornish and Liu, Arxiv 1803.01944
INPUT:
freq– frequency \(f\) (in \(\mathrm{Hz}\))
OUTPUT:
effective power spectral density \(S(f)\) (in \(\mathrm{Hz}^{-1}\))
EXAMPLES:
sage: from kerrgeodesic_gw import lisa_detector sage: Sn = lisa_detector.power_spectral_density_RCLfit sage: Sn(1.e-1) # tol 1.0e-13 2.12858262120861e-39 sage: Sn(1.e-2) # tol 1.0e-13 1.44307343517977e-40 sage: Sn(1.e-3) # tol 1.0e-13 1.63410027259543e-38
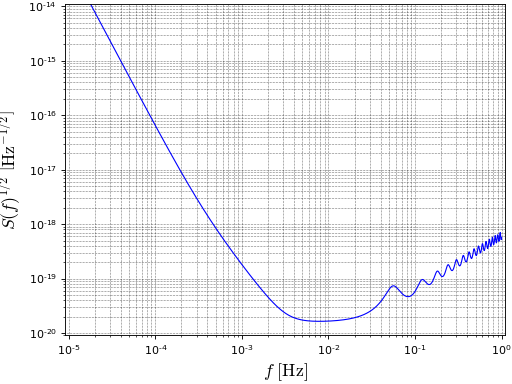
- kerrgeodesic_gw.lisa_detector.strain_sensitivity(freq)¶
Return LISA strain spectral sensitivity at a given frequency.
The strain spectral sensitivity is the square root of the effective noise power spectral density (cf.
power_spectral_density()).INPUT:
freq– frequency \(f\) (in \(\mathrm{Hz}\))
OUTPUT:
strain sensitivity \(S(f)^{1/2}\) (in \(\mathrm{Hz}^{-1/2}\))
EXAMPLES:
sage: from kerrgeodesic_gw import lisa_detector sage: hn = lisa_detector.strain_sensitivity sage: hn(1.e-1) # tol 1.0e-13 5.82615031500758e-20 sage: hn(1.e-2) # tol 1.0e-13 1.654806317072275e-20 sage: hn(1.e-3) # tol 1.0e-13 1.8082609253700212e-19
sage: plot_loglog(hn, (1e-5, 1), plot_points=2000, ymin=1e-20, ymax=1e-14, ....: axes_labels=[r"$f\ [\mathrm{Hz}]$", ....: r"$S(f)^{1/2} \ \left[\mathrm{Hz}^{-1/2}\right]$"], ....: gridlines='minor', frame=True, axes=False) Graphics object consisting of 1 graphics primitive